Authors: Felix B. A. Tellander, Johan E. M. Ulander, Irina I. Yakimenko, Karl-Fredrik Berggren
Institution: Department of Astronomy and Theoretical Physics, Lund Univer- sity, SE- 223 62 Lund, Sweden; Department of Mathematical Sciences, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden; Department of Physics, Chemistry and Biology (IFM), Linköping University, SE-581 83 Linköping, Sweden
doi:10.22186/jyi.31.4.1-6
ABSTRACT
The structure of scattered wave fields and currents is of interest in a variety of fields within physics such as quantum mechanics and optics. Traditionally two-dimensional structures have been investigated; here we focus on three-dimensional structures. We make a generic study of three dimensional quantum box cavities, and our main objective is to visualize the probability current. Visualizations are achieved for complex linear combinations of wave functions with different excitations and with boundary conditions: Dirichlet, Neumann, and mixed. By using different boundary conditions, the results reported here are relevant to many different wave analogues such as microwave billiards and acoustic cavities. Visualization was mainly done through animated images, but a chaotic state was visualized by 3D printing. Our results suggest that if the state of excitation is the same in the different boundary conditions, the current is the same, except at the boundaries of the box. Application to sort nanoparticles in acoustic cavities is considered.
INTRODUCTION
Mapping and understanding the structure of wave fields and currents is relevant to a variety of structures such as quantum structures, optical and acoustic cavities, microwave billiards and water waves in a tank (Berggren & Ljung, 2009; Berggren, Yakimenko, & Hakanen, 2010; Blümel, Davidson, Reinhardt, Lin, & Sharnoff, 1992; Stöckmann , 1999; Chen, Liu, Su, Lu, Chen, & Huang, 2007; Ohlin & Berggren, 2016; Panda & Hazra, 2014). Here, cavities and billiards stand for systems with hard walls such that a particle or a wave only scatter from the walls and there is no scattering within the system. Acoustic cavities are metal enclosed cavities where a microphone is used to emit the waves. The underlying physics of all these systems is seemingly different. For example, in acoustic cavities, the waves are pressure differences in the air. In quantum cavities, the waves are the particles themselves. Nevertheless, the wave nature of these phenomena is often equivalent because it is governed by the Helmholtz equation (Stöckmann, 1999). Although there has been much progress within the fabrication of heterostructures, where quantum mechanical phenomena can be directly observed and measured, they are still difficult to manipulate. The different wave analogues are therefore important supplements for the experimental realization of quantum structures since they are easier to handle. Optical and laser cavities have recently been used for studying the concept of space-time reflection symmetry (Brandstetter et al., 2013; Liertzer et al., 2012) developed by Bender, Boettcher and Meisinger (Bender & Boettcher, 1998; Bender, Boettcher, & Meisinger, 1999) as an extension of Hermitian quantum mechanics. Acoustic and microwave cavities have been used to study exceptional points (Dembowski, et al., 2001; Ding, Ma, Xiao, Zhang, & Chan, 2016) which are points where the eigenvalues of two states are equal and their corresponding eigenvectors just differ by a phase (Rotter, 2009). Microwave cavities have also been important in the development of quantum chaos (Sadreev & Berggren, 2005; Stöckmann, 1999); the study of quantum systems that in the classical limit is chaotic i.e. a change in the initial conditions leads to exponential divergence of the trajectories in phase space.
Earlier studies, especially of quantum structures, have focused on two-dimensional fields because they are easier to study experimentally. However, a more realistic theoretical model would need to take all three dimensions into account (Ferry, Goodnick, & Bird, 2009). In this paper, we model three-dimensional quantum billiards with different boundary conditions and study the structure of the probability current for states of different excitations. Because different boundary conditions in the modeling were employed, the results are also applicable to the other wave analogues. The probability current is a three-dimensional vector field, which is difficult to visualize. Therefore, we also study the nodal surfaces and nodal lines. Nodal surfaces are surfaces where either the real or the imaginary part of the wave function is zero and the nodal lines are the intersection between the nodal surfaces (i.e., where both the real and imaginary parts are zero). The current will create vortices around these lines (Dirac, 1931; Wyatt, 2005). If the distribution of vortices is known, the overall structure of the current is known. The appearance and location of vortices have been directly connected to minima in the conductance i.e. the transmission through two-dimensional quantum structures (Lundberg, Sjöqvist, & Berggren, 1998) and the vortex distribution can be used to determine whether a system is chaotic (Saichev, Berggren, & Sadreev, 2001).
METHODS
Calculations
To map the probability current, a quasi-analytic method based on separation of variables and the finite difference method (FDM) is used. The ordinary time-dependent Schrödinger equation
(Merzbacher, 1998) for the wave function
is:
(1)
Since the potential function V(r) does not depend time, we may write the wave function as:
(2)
where E is the energy of the state and
Schrödinger equation:
satisfies the time-independent
(3)
We now introduce the coefficient
and use the model of a particle in a
box, where V = 0 inside the box and is infinite outside. [Eq. (3)] can now be written as the Helmholtz equation:
(4)
The solutions can be expressed as Fourier series. Depending on the boundary conditions, the series will contain sine, cosine or both. For example, a box with side lengths a, b, and c, all with Dirichlet
boundary condition (i.e.,
on the boundaries), has the series:
(5)
where the square root is due to normalization and are Fourier coefficients. If the boundary condition is changed to Neumann in one direction (i.e., instead of putting the wave function to zero at the boundaries in this direction, we set the derivative of the wave function to zero) the sine factor in this direction is changed to cosine.
Conservation of electrical charge entails that if the amount of charge in a system is changed there must exist a current responsible for this change. Similarly, probability current is obtained due to the conservation of probability; if the probability density of the system is changed there must exist a probability current mediating this change. For both probability and charge, the continuity equation reads,
(6)
where
is the density function and j is the current vector.
Note that both p and j are time-independent because of [Eq. (2)]. From [Eq. (6)] and [Eq. (3)], one obtains the following expression for the probability current:
This expression is evaluated numerically by a finite-difference approximation of the
(7)
gradients. We choose units such that
Visualization
The Fourier series in [Eq. (5)] with sine and/or cosine terms can express the solution for different boundary conditions. From this expression, the nodal surfaces are easily found by standard routines (iso-surface) in MATLAB (MATLAB, 2012). Because of the simplicity of calculating the nodal surfaces, we will mostly visualize them throughout this work. Finding the nodal lines, which are more directly connected to the current, is a much more difficult problem. However, it is analytically solvable for some simple cases. One of the easiest cases arises when the Fourier series only contains two terms, one real and one imaginary, such that one of the terms contains two trigonometric factors in the ground state and only one excited factor and vice versa for the other term. That means, for the case with Dirichlet boundary condition, that two of the numbers (say n and l) is equal to one while m > 1, and n, l > 1 and m = 1 for the other, i.e.,
(8)
With Neumann boundary condition all the numbers are decreased by one. This case is solvable because the nodal surfaces will be orthogonal sheets with straight orthogonal intersections (Figures 1 and 2). The position of these lines can be found directly by reading the wave function. For more complicated cases the nodal lines can be found by an algorithm presented by Ljung and Ynnerman (2003). To obtain a clearer picture of the structure of the nodal surfaces, we 3D-printed the surfaces for a chaotic wave function.
RESULTS
Neumann Boundary Condition
We begin with a state under Neumann boundary condition:
(9)
This represents one of the cases previously mentioned in which the nodal lines can be found directly because of the simple structure of the nodal surfaces (Figure 1A). There are six nodal lines to this state: three in the x-direction and three in the y-direction (Figure 2). The nodal lines in the x-direction are parameterized by (x, b(1+2n)/6, c/2) where n = 0,1,2. The nodal lines in the y-direction are parameterized similarly. Vortices are observed around these lines (Figure 2B-D).
Figure 1. Nodal lines and probability current for [Eq. (9)]. Nodal lines and a part of the probability current for the state in [Eq. (9)].
Figure 2. Nodal surfaces and probability current for [Eq. (9)]. (A) Nodal surfaces for the state in [Eq. (9)] with Neumann boundary condition are shown. The horizontal plane is for the real part and the vertical are for the imaginary. (B-D) Probability current viewed from three different directions where the x-, y-, and z-axes show the special dimensions of the box.
Dirichlet and Mixed Boundary Conditions
Here we study states corresponding to the same state of excitation as the state in [Eq. (9)] but now with Dirichlet and mixed boundary condition. The corresponding state with Dirichlet boundary condition is:
(10)
Note that because of the boundary condition, the wave function is zero on every side of the box. For the sake of visualization, these parts of the nodal surfaces have been removed (Figure 3A). The nodal lines for this state in the x-direction are parameterized by (x, bn/4, c/2) with n = 1,2,3 and similarly in the y-direction. The current propagates in vortices around these lines (Figure 3B-D).
Figure 3. Nodal surfaces and probability current for [Eq. (10)]. (A) Nodal surfaces for the state in [Eq. (10)] with Dirichlet boundary condition. (B-D) Obtained probability current is viewed from three different directions.
We choose the mixed boundary condition such that it is Dirichlet in the x- and y-directions and Neumann in the z-direction. This state is given by:
(11)
and the nodal surfaces and current are shown in (Figure 4A-D).
Figure 4. Nodal surfaces and probability current for [Eq. (11)]. (A) Nodal surfaces for the state in [Eq. (11)] with Dirichlet boundary condition are displayed. (B-D) Obtained probability current is viewed from three different directions.
To represent the structure of higher order states, we visualize three states with higher excitations (Figure 5A-C). These states are given by [Eq. (12)], [Eq. (13)] and [Eq. (14)] respectively and each has one of the studied boundary conditions. The state given by:
(12)
is with Neumann boundary condition and
(13)
is with Dirichlet boundary condition. The last state is with mixed conditions.
(14)
Figure 5. Different examples of nodal surfaces. Nodal surfaces for the states in (A) Equation (12), (B) Equation (13) and (C) Equation (14) are shown. For this simple case with only two terms in the Fourier series, the higher excitation in a direction is observed as more sheets in that direction.
Using more terms in the linear combination the surfaces becomes more complex. For example:
(15)
For this state, the nodal surfaces are visualized both as animated figures and 3D-printed models (Figure 6A-D).
Figure 6. Simulated and 3D printed complex nodal surfaces. Nodal surfaces for the state in [Eq. (15)] are shown. (A) is the real part and (B) is the imaginary part. (C-D) 3D-printed versions of the same surfaces are displayed.
Particle Separation
We simulate particle separation in an acoustic cavity for which the appropriate boundary condition is Neumann (Morse, 1948). To do the simulation, a very simple state with only one nodal line (Figure 7A) is employed
(16)
We now place two particles with mass ratio 1:10 at the top of the box near the nodal line. They are affected both by the gravitational force and a pressure force obtained by the current. The trajectories of the two particles are clearly different (Figure 7B). The heavy particle is much less affected by the current. Thus, in a scenario with many particles, the heavy particles would be found near the center of the box while the lighter particles would be located at the boundaries.
Figure 7. Simulation of particle sorting. (A) Current used in the simulation of particle separation is shown. This current corresponds to the state in [Eq. (16)]. (B) Simulation of particles with mass ratio 1:10 demonstrates that particles begin at the same point but end up at different points.
DISCUSSION AND CONCLUSION
The main objective of this work was to map the three-dimensional structure of probability currents and nodal surfaces in box cavities. By using different boundary conditions, the results obtained here are not only relevant for quantum cavities but also for microwave and acoustic cavities. A chaotic state was visualized by 3D printing. We suggest that these currents can be used for particle separation in acoustic cavities.
Three states with the same order of excitation [Eq. (9)], [Eq. (10)], and [Eq. (11)] were studied. We conclude that although different boundary conditions are used, the structure of the current is similar (Figures 2, 3, and 4). The obtained current for Neumann boundary condition (Figure 2) shows full agreement with the results in the recent experimental study by Ohlin and Berggren (2016). The findings could be used to simplify the modeling of complex structures in quantum transport calculations. When calculating the transmission through a quantum system one should in principle take an infinite number of states into account. This is numerically not possible so the number of states must be truncated. For transmission calculations using an effective non-Hermitian Hamiltonian it has been shown that only the case with Neumann boundary condition is stable with a finite number of states (Pichugin, Schanz, & Seba, 2001). If the physical importance of the boundary conditions can be relaxed, effective non-Hermitian Hamiltonians could be used with Dirichlet boundary condition for cases when Neumann seems like the natural boundary condition (Lee & Reichl, 2010).
We simulated particle separation in an acoustic cavity and observed a clear separation of particles with mass ratio 1:10. However, the current model is only conceptual and in need of improvements. Future research should take into account the shape and spin of the particles. One should also consider that the particles are present in the cavity and hence affect the structure of the current. These observations should be included in the Navier-Stokes equations and thus a fluid dynamic description of the system is obtained.
ACKNOWLEDGEMENTS
We would like to thank Magnus Sethson and David Beuger at the Department of Management and Engineering at Linköping University for providing access to their 3D-printers.
REFERENCES
Ahrén, M. (2013). Metal Oxide Nanoparticles for Contrast Enhancement in Magnetic Resonance Imaging. Doctoral dissertion, Linköping University. doi:10.3384/diss.diva-98693.
Bender, C. M., & Boettcher, S. (1998). Real Spectra in Non-Hermitian Hamiltonians Having PT-Symmetry. Physical Review Letters, 80(24), 5243-5246. doi:10.1103/PhysRevLett.80.5243.
Bender, C. M., Boettcher, S., & Meisinger, P. N. (1999). PT-symmetric quantum mechanics. Journal of Mathematical Physics, 40(5), 2201-2229. doi:10.1063/1.532860.
Berggren, K. F., & Ljung, P. (2009). Nature of streamlines for Berry-type wavefunctions in open 3D cavities. Mathematical modeling of wave phenomena, American Institute of Physics, 1106, 253-259. doi:10.1063/1.3117101.
Berggren, K. F., Yakimenko, I. I., & Hakanen, J. (2010). Modeling of open quantum dots and wave billiards using imaginary potentials for the source and the sink. New Journal of Physics, 12, doi:10.1088/1367-2630/12/7/073005.
Blümel, R., Davidson, I. H., Reinhardt, W. P., Lin, H., & Sharnoff, M. (1992). Quasilinear ridge structures in water surface waves. Physical Review A, 45(4), 2641-2644. doi:10.1103/PhysRevA.45.2641.
Brandstetter, M., Liertzer, M., Deutsch, C., Klang, P., Schöberl, J., Türeci, H. E., . . . Rotter, S. (2013). Reversing the pump dependence of a laser at an exceptional point. Nature Communications 5, doi:10.1038/ncomms5034.
Chen, C. C., Liu, C. C., Su, K. W., Lu, T. H., Chen, Y. F., & F, H. K. (2007). Statistical properties of experimental coherent waves in microcavity lasers: Analogous study of quantum billiard wave functions. Physical Review E, 75(4), doi:10.1103/PhysRevE.75.046202.
Dembowski, C., Gräf, H.-D., Harney, H., Heine, A., Heiss, W., Rehfeld, H., & Richter, A. (2001). Experimental Observation of the Topological Structure of Exceptional Points. Physical Review Letters, 86(5), 787-790. doi:10.1103/PhysRevLett.86.787.
Ding, K., Ma, G., Xiao, M., Zhang, Z., & Chan, C. (2016). Emergence, Coalescence, and Topological Properties of Multiple Exceptional Points and Their Experimental Realization. Physical Review X, 6(2), doi:10.1103/PhysRevX.6.021007.
Dirac, P. A. (1931). Quantised Singularities in the Electromagnetic Field. Proceedings of the Royal Society A, 133(821), 60-72. doi:10.1098/rspa.1931.0130.
Ferry, D. K., Goodnick, S. M., & Bird, J. (2009). Transport in Nanostructures. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511840463.
Lee, H., & Reichl, L. E. (2010). R-matrix theory with Dirichlet boundary conditions for integrable electron waveguids. Journal of Physics A: Mathematical and Theoretical, 43(40), doi:10.1088/1751-8113/43/40/405303.
Liertzer, M., Ge, L., Cerjan, A., Stone, A. D., Türeci, H. E., & Rotter, S. (2012). Pump-Induced Exceptional Points in Lasers. Physical Review Letters, 108(17), doi:10.1103/PhysRevLett.108.173901.
Ljung, P., & Ynnerman, A. (2003). Extraction of Intersection Curves from Iso-surfaces on Co-Located 3D grids. The Annual SIGRAD Conference. Special Theme – Real-Time Simulations (pp. 23-28). Linköping: Linköping University Electronic Press. doi:10.1.1.114.510.
Lundberg, T., Sjöqvist, E., & Berggren, K.-F. (1998). Analysis of electron transport in a two-dimensional structure using quantal trajectories. Journal of Physics: Condensed Matter: Condensed Matter, 10(25), 5583-5594. doi:10.1088/0953-8984/10/25/010.
MATLAB. (2012). version R2012a. Natick, Massachusetts: The MathWorks Inc.
Merzbacher, E. (1998). Quantum mechanics. New York: Wiley.
Morse, P. M. (1948). Vibration and Sound. McGraw-Hill.
Ohlin, K., & Berggren, K. F. (2016). Patterns beyond Faraday waves: observation of parametric crossover from Faraday instabilities to the formation of vortex lattices in open dual fluid strata. European Journal of Physics, 37(4), doi:10.1088/0143-0807/37/4/045803.
Panda, P., & Hazra, G. (2014). Boundary perturbations and the Helmholtz equation in three dimensions. The European Physical Journal Plus, 129(53), doi:10.1140/epjp/i2014-14053-y.
Pichugin, K., Schanz, H., & Seba, P. (2001). Effective coupling for open billiards. Physical Review E, 64(5), doi:10.1103/PhysRevE.64.056227.
Rotter, I. (2009). A non-Hermitian Hamiltonian operator and the Physics of open quantum systems. Journal of Physics A: Mathematical and Theoretical, 42(15), doi:10.1088.1751.8113.42.15.153001.
Sadreev, A. F., & Berggren, K.-F. (2005). Signatures of quantum chaos in complex wavefunctions describing open billiards. Journal of Physics: Mathematical and Generla, 38(49), 10787-10804. doi:10.1088.0305-4470.38.49.019.
Saichev, A. I., Berggren, K.-F., & Sadreev, A. F. (2001). Distribution of nearest distances between nodal points for the Berry function in two dimensions. Physical Review E, 64(3), doi:10.1103/PhysRevE.64.036222.
Stöckmann, H. J. (1999). Quantum chaos. Cambridge: Campridge University Press.
Wyatt, R. E. (2005). Quantum Dynamics with Trajectories. Springer.
















![Figure 1. Nodal lines and probability current for [Eq. (9)]. Nodal lines and a part of the probability current for the state in [Eq. (9)].](https://images.squarespace-cdn.com/content/v1/5443d7c7e4b06e8b47de9a55/1487369175754-HBW5O5RB58JEPVMKANLY/image-asset.png)
![Figure 2. Nodal surfaces and probability current for [Eq. (9)]. (A) Nodal surfaces for the state in [Eq. (9)] with Neumann boundary condition are shown. The horizontal plane is for the real part and the vertical are for the imaginary. (B-D) Probabil…](https://images.squarespace-cdn.com/content/v1/5443d7c7e4b06e8b47de9a55/1487369182812-AYCS7OPBP409Y7HLVSCN/probability+current+fig+2.png)

![Figure 3. Nodal surfaces and probability current for [Eq. (10)]. (A) Nodal surfaces for the state in [Eq. (10)] with Dirichlet boundary condition. (B-D) Obtained probability current is viewed from three different directions.](https://images.squarespace-cdn.com/content/v1/5443d7c7e4b06e8b47de9a55/1487369189664-4VVC5QFJ3BORKBNQCG6H/image-asset.png)
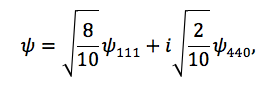
![Figure 4. Nodal surfaces and probability current for [Eq. (11)]. (A) Nodal surfaces for the state in [Eq. (11)] with Dirichlet boundary condition are displayed. (B-D) Obtained probability current is viewed from three different directions.](https://images.squarespace-cdn.com/content/v1/5443d7c7e4b06e8b47de9a55/1487369590620-B01XUCHROBV8L8BPTEMD/probability+current+fig+4.png)





![Figure 6. Simulated and 3D printed complex nodal surfaces. Nodal surfaces for the state in [Eq. (15)] are shown. (A) is the real part and (B) is the imaginary part. (C-D) 3D-printed versions of the same surfaces are displayed.](https://images.squarespace-cdn.com/content/v1/5443d7c7e4b06e8b47de9a55/1487370270127-DPBEI28XDKII0JXCYZE0/probability+current+fig+6.png)
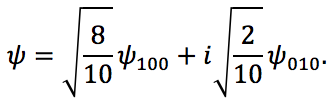
![Figure 7. Simulation of particle sorting. (A) Current used in the simulation of particle separation is shown. This current corresponds to the state in [Eq. (16)]. (B) Simulation of particles with mass ratio 1:10 demonstrates that particles begin at …](https://images.squarespace-cdn.com/content/v1/5443d7c7e4b06e8b47de9a55/1487370401656-KWXDO55YFY6E5GUAB9PL/image-asset.png)