Author: Christina Brandt
Institution: Cornell University
Date: September 2008
ABSTRACT
Electronic noses, small electronic instruments with carbon sensing films, provide an artificial version of our olfactory system. In conjunction with pattern recognition techniques, electronic noses can be used to identify odor combinations, perform rudimentary perceptual analysis, and classify unknown odors. Although many different algorithms, from statistical analysis to biologically-inspired neural networks, have been implemented as e-nose pattern recognition techniques, no perfect algorithm has been found. This paper explores the creation and implementation of a novel identification system that uses an outside database to extrapolate the identity of an unknown odor. The algorithm utilizes Principle Component Analysis, clustering, and a k-nearest neighbors algorithm based on chemical similarities, and is found to be 100% accurate for correlating the identity of scents with approximately the same reactance mean as known chemicals. However, due to an oversimplification of representation of chemicals in the external database, it has performed with 20% accuracy in extrapolating the identity of unknowns. With more accurate data, a complex representation of chemicals, and a larger data set, the algorithm could potentially achieve high accuracy in hypothesizing the identity of unknowns. Such an algorithm can be used in environmental, military, and medical applications because it provides an unsupervised learning component to classification that can be used to contend with unexpected events.
INTRODUCTION
The olfactory sense is constantly underestimated by humans. The sense of smell provides identification of countless chemicals, supplies qualitative and quantitative information, and even influences human perceptions (Loutfi 2006). Electronic noses, or e-noses, provide a way of artificially utilizing the powerful tool of olfaction. E-noses are small electronic instruments made from polymer carbon composite sensing films which are doped with different materials (Ryan et al. 2004). When the e-nose "sniffs" a scent, the films swell or contract, changing the electrical resistance in the sensors (Goodman and Tang 2005). The variations in electrical resistance are then sent to a pattern recognition algorithm to be analyzed. Since each doped sensor in the array reacts differently, the sensor provides an "electronic fingerprint" for each odor (Llobet 2003). The pattern recognition algorithms use this information to perform identification and classification
Pattern recognition techniques, or "PARCs," analyze the data provided by the sensors and transform the arrays of resistance changes to powerful sets of information which can be used to diagnose diseases, control quality in food, monitor the environment, and even assure safety by detecting toxins (Llobet 2003). With the correct type of pattern analysis, electronic noses can be used to identify odor combinations, perform rudimentary perceptual analysis, and even classify unknown odors (Burl et al. 2002). A host of algorithms have been applied to the electronic nose problem, from statistical analysis techniques such as Principle Component Analysis to non-parametric analysis involving artificial neural networks (Hines et al. 2003). Most algorithms must undergo a training phase in which samples with known classifications or groupings are utilized to "teach" the algorithm the correct classifications (Carmel et al. 2003). The type of algorithm determines the level of human supervision and the amount of information that this training phase requires. Once the algorithm is trained, it can identify an unknown odor as a member or mixture of the categories that it was trained to recognize. Effective algorithms should be accurate, fast, easy to train, have low memory requirements, and be resilient to noise and baseline drift (Carmel et al. 2003). No perfect algorithm exists for olfactory analysis because of these tight specifications. Neither statistical analysis nor biologically-inspired models can fulfill all requirements. The strengths and weakness of several techniques used in olfactory analysis will be discussed in the following paragraphs.
Statistical analysis is often fast in practice and does not require a training phase. Its conclusions are closely tied to the data and the reactant nature of the chemicals involved, removing the danger of training-related errors. However, statistical analysis often depends heavily on the assumption that data is linear (Loutfi 2006). Although sensor data tends to be linear over certain periods, at higher concentrations the data quickly leaves the realm of predictability, causing linearly-dependent algorithms to function inaccurately (Hines et al. 2003). Even non-linear statistical algorithms function by grouping data according to some mathematical function from which data may deviate at high concentrations.
One of the most commonly utilized forms of statistical analysis is Principle Component Analysis (PCA). PCA is an unsupervised form of pattern analysis that expresses response vectors in terms of linear combinations of "Principle Components": orthogonal eigenvectors that contain most of the data variance (Smith 2002). PCA allows simplification of data and removal of noise. However, it does not provide classification or identification. Another algorithm, such as cluster analysis, must be used on PCA-processed data (Smith 2002). However, because of its effectiveness at dimensional reduction, noise removal, and scaling, PCA is often used as a preprocessing technique (Brezmes et al. 2005).
Cluster analysis is an unsupervised, non-parametric technique that is used to discriminate between response vectors by enhancing their differences. Since clusters can be altered dynamically, the model undergoes unsupervised learning (Lian and Tan 2004). Multiple techniques are classified under the heading of cluster analysis, including agglomerative hierarchical clustering, in which data is grouped into a dendogram or binary tree (Lian and Tan 2004). This method successively merges the closest two clusters until only a single cluster remains. Although useful for hierarchical analysis, it is somewhat inefficient if order is unimportant. Another form of cluster analysis is k-means, in which the programmer specifies a number of clusters and the algorithm breaks the data into these clusters (Tryfos 1998). For the purpose of identification using an external database, this algorithm is severely limiting, since it requires the user to specify the number of clusters from the outset.
A more flexible form of cluster analysis is density-based clustering, in which a cluster is represented by a dense centroid region surrounded by an area of lower density (Kumar et al. 2006). Density-based clustering often utilizes a technique called K-Nearest Neighbor, or kNN, analysis. This calculates the distance between responses using a specified distance measure, then assigns the unknown to its nearest neighbor (Vaid et al. 2001). However, finding the kNN can be expensive in both speed and memory requirements. Several algorithms exist to minimize the time constraints of finding the nearest neighbor, including the grouping of data into kd-trees (Yianilos 2000). Kd-trees arrange multidimensional data by planar partitioning (Moore 1991). While they are inefficient for more than eight dimensions, kd-trees perform more economically than simple linear searching (Moore 1991). Although density-based cluster analysis presents problems in implementation and can be sensitive to baseline drift, it is ideal for realistic situations because it does not require input such as the number of groups and does not force the artificial order that agglomerative hierarchical clustering requires (Lian and Tan 2004).
Another form of data classification utilizes biologically-inspired artificial neural networks. Unlike statistical analysis, neural networks do not require linearity or adherence to a mathematical model (Brezmes et al. 2003). They can also be used to perform "fuzzy analysis," a technique that allows odors to be grouped into vague linguistic categories that mimic human perception. "Fuzzy analysis" provides results that cannot be easily achieved with statistical techniques, including "quality assessments" of odors that mimic human perception (Brezmes et al. 2005). However, neural networks are not without faults. They often require the programmer to initially determine a fixed number of groups for classification (Hines et al. 2003). This means that although neural networks act as learning algorithms, it is extremely difficult to train them to recognize new scents once they have finished their training phase (Burl et al. 2002). Neural networks can also be over-trained when too many samples are used during the training phase. This over-training can destroy their usefulness and often cannot be amended without completely retraining the network, which is a time-consuming and difficult process. Despite the advantages of neural networks, they can often be less efficient and productive than statistical analysis.
Algorithms are often tailored to the particular type of identification for which they are utilized. Fuzzy neural networks are best for perceptual analysis, while statistical algorithms often handle concentration effectively (Hines et al. 2003). Both neural networks and statistical analysis have been applied to scent and mixture identification, in which an "unknown" odor is classified either as a particular known scent or as a mixture of two or more known scents. However, the algorithm is obviously limited to describing odors by its initial "training set" of known entities. Ideally, an algorithm should examine an unknown in the context of known factors, classify it, and use it to analyze new odors. This paper proposes an algorithm that uses an external database to extrapolate the identity of an unknown sample, then "learns" this odor in continued analysis. Such an algorithm could be extremely useful in "real-life" situations in which the e-nose is used to make fast decisions based upon its knowledge. In such a case, returning to the lab and extending the training phase would not be possible. By using an algorithm that evaluates through common structures and factors, a robot equipped with the sensor could react to identifications of potentially dangerous chemicals that it was not previously trained with. The algorithm described in this paper uses a dynamic-learning system implemented with cluster analysis and k-nearest neighbor searching, which accesses an external chemical database to extrapolate the identity of a previously unknown chemical. The goal of the project was to implement a robust, efficient system that would not only correctly classify odors previously learned, but also hypothesize the identity of an unknown odor.
MATERIALS AND METHODS
The algorithm is programmed in MATLAB and utilizes multiple probabilistic techniques and an external chemical database to analyze input electronic sensor data. It can be trained with a representative set of substances with various chemical compositions and functional groups at various concentrations. Each substance is categorized as a different cluster, which defines a density-based cluster analysis method for the working phase. Once it is trained, the algorithm creates a cluster for an unknown chemical and compares it with the known chemical clusters. It then determines the k-number of clusters in which the unknown cluster is probabilistically most likely to reside. Once these "k nearest neighbors" have been determined, the algorithm compares their structures, finds similarities, and assigns each a confidence factor. It then searches the external database to find the chemical with the highest sum of scaled confidence factors and identifies the unknown cluster as this chemical.
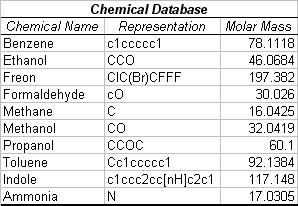
Since no functional electronic nose existed in our laboratory, data was utilized from the Jet Propulsion Laboratory (JPL) research group's e-nose for initial tests., Cluster simulations were also created using data extrapolated from graphs of mean resistance data from the JPL group paper, "Nonlinear Least-Squares Based Method for Identifying and Quantifying Single and Mixed Contaminants in Air with an Electronic Nose" (Zhou et al. 2006; Table 1).
Table 1. Chemical Database. The database provides the chemical name, a simplified linearized structure, and the molar mass of each of the ten chemicals shown. Cluster simulations were created using data extrapolated from graphs of mean resistance data from the Jet Propulsion Laboratory electronic nose paper, "Nonlinear Least-Squares Based Method for Identifying and Quantifying Single and Mixed Contaminants in Air with an Electronic Nose" (Zhou et al. 2006). The chemical structures are represented in Simplified Molecular Input Line Entry Specification format (SMILES).
A small external chemical database was also created with information such as the chemical name, molecular weight, and a simple linearized representation of its structure. The algorithm utilizes two-stages to extrapolate a chemical identity from the resistance data and external database provided: a training phase and an operational phase (Figure 1).
Figure 1. Schematic of Program Phases. In the training phase, all chemicals are analyzed before PCA is performed. The operational phase then uses the PCA scaling matrix, the original clusters, and an external database to perform a structural comparison to infer the chemical identity of an unknown. The chemical clusters used in this trial were simulated with data extrapolated from graphs (Zhou et al. 2006).
In the training stage, the algorithm undergoes supervised learning. It accepts an array of sensor data from the electronic nose along with the name of the compound. Once the training set of data points of various chemicals is input into the program, the program performs PCA analysis to scale data down from the initial number of dimensions, which typically ranges from eight to thirty-two, to a user-input dimension, typically three. The PCA analysis returns a transformation matrix through which other incoming matrices in the operational phase can be scaled to the same space. It also returns a new matrix of PCA-scaled values of the training data, which is used to create a data cluster for each chemical (Figure 2).
Figure 2. Graph of Training Phase Output. Each of the chemicals is scaled through PCA to three dimensions from thirty-two. The centroid, variance, and number of points are determined and saved in the cluster. The initial points are discarded to save memory. The chemical clusters used in this trial were simulated with data extrapolated from graphs (Zhou et al. 2006).
Each cluster contains data such as the chemical's name, the centroid of the cluster, its variance, the number of points it holds, and the chemical structure, which is determined from the external database.
Once the program is trained to an initial set of chemicals, the operational phase begins. In the operational phase, unknown chemical sensor data is input into the system in the same fashion as the training data. PCA scaling and rotation transformations are then applied to the new matrix of data so that it occupies the same space as the training phase-created clusters. This data is represented as a PointCluster, which stores its initial points, unlike the clusters representing identified chemicals (Figure 3).
Figure 3. Graph of PointCluster in relation to Known Clusters. Each of the known clusters is represented by its name and centroid. The unknown PointCluster, in actuality Ethanol, is represented by the green dots. PointClusters retain their data points for centroid and variance calculations for analysis later in the process. The chemical clusters used in this trial were simulated with data extrapolated from graphs (Zhou et al. 2006).
Using the cluster form, the unknown can then be represented spatially by its centroid.
The unknown chemical is then mapped alongside the known clusters. The clusters with the highest probability of containing the centroid are then found. This probability calculation is done using Chebyshev's inequality, which states that the probability from the distance is less than or equal to the variance over the square of the distance (Equation 1).
Equation 1. Chebychev's Inequality. This equation describes the probability that a value exists at a location greater than or equal to some distance from its expected value. It states that the probability that the random variable X has a value greater than k from its mean is the variance of X over the square of k.
Each cluster is assigned a "confidence" that the unknown chemical appears in that cluster equal to the variance over the square of the distance between them. The k-number of compounds with the highest confidence factors are then returned to the main program for feature processing.
In the feature processing step, each combination of substrings are searched to find common features, which are then searched again to find three or more compounds containing these substrings. The confidence factor of a substring is the sum of the confidences of its members multiplied by a factor relating to the size of the substring. These substrings are then sorted in decreasing order of their confidence factors.
Next, the molar mass of the compound and its deduced structure are used as factors to locate similar compounds. The database is searched to find the compound with the largest sum of confidence factors from the substring. This compound confidence is also weighted by comparing the mean of the nearest neighbors' molar masses to the molar mass of the compound. The compound with the highest calculated confidence is considered to be the identification match for the unknown chemical. This result is returned to the main program, which then "learns" the compound according to the nature of the identification. If the identification match has already been made into a cluster, the points from the new cluster will be added to it and the centroid and variance will be recalculated. If the unknown has been identified as a new chemical, a new cluster will be created to represent it (Figure 4).
Figure 4. Representation of Newly Recognized Clusters. The algorithm has correctly identified the unknown cluster as Ethanol. It now creates a cluster to represent Ethanol, discards the points, and continues analysis. The chemical clusters used in this trial were simulated with data extrapolated from graphs (Zhou et al. 2006).
The program reports these changes, and is then ready to accept a new operational data set.
RESULTS
Testing and analysis of the algorithm proved to be extremely difficult. Since no access to a working electronic nose system existed, no "real" data existed for testing purposes; therefore the results may not be representative of the algorithm's actual performance. The algorithm was assessed on data extrapolated from graphs of mean resistance data from the JPL group paper, "Nonlinear Least-Squares Based Method for Identifying and Quantifying Single and Mixed Contaminants in Air with an Electronic Nose," (Table 1). This data was also supplemented with four chemical data sets from past electronic nose trials performed by the Jet Propulsion Laboratory Electronic Nose research group (Ryan, Dr. Margaret Amy, personal communication 2007). Due to the noise and limited nature of the raw data provided, it was used for validation rather than analysis.
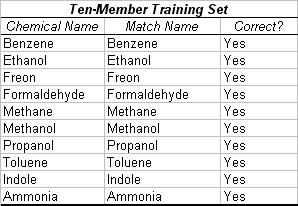
The algorithm was tested in two methods of cross-validation. First, the entire ten-member extrapolated data set was entered as a training set, and a similar, smaller cluster with approximately the same mean centroid as one member of the training set was entered in the operational stage. The operational stage, when processing a 100 x 32 matrix of extrapolated resistance data, was found to have a duration of less than one hundredth of a second. In 100% of the cases, the algorithm successfully recognized the previously identified chemical (Table 2).
Table 2. Trial with Ten-Member Training Set. In this trial, all chemicals were entered in the training set. Then a smaller cluster with an almost identical centroid to one of the existing chemicals was input in the operational phase. The algorithm correctly determined the identity of each chemical, leading to an accuracy of 100% in this case. The simulated chemical clusters were extrapolated from "Nonlinear Least-Squares Based Method for Identifying and Quantifying Single and Mixed Contaminants in Air with an Electronic Nose" (Zhou et al. 2006).
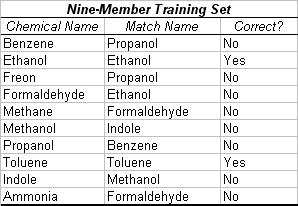
A second test was then performed to test the efficacy of the algorithm's ability to extrapolate a chemical identity. In ten separate tests, nine chemicals were entered in the training phase. The tenth was then entered in the operational stage, and the identity hypothesized by the algorithm was then compared to the actual identity of the chemical. The algorithm was found to have approximately 20% accuracy in determining the identity of the unknown chemical in this case (Table 3).
Table 3. Trial with Nine-Member Training Set. In this trial, nine of the ten chemicals were entered in the training set. The tenth chemical was then presented in the operational stage. The algorithm was supposed to extrapolate the identity of the unknown from the similar molecular substructures of surrounding chemicals. However, possibly due to the limited training set, the test resulted in 20% accuracy. The simulated chemical clusters were extrapolated from "Nonlinear Least-Squares Based Method for Identifying and Quantifying Single and Mixed Contaminants in Air with an Electronic Nose" (Zhou et al. 2006).
DISCUSSION AND CONCLUSIONS
Efficiency, accuracy, and practicality were the main concerns for the preliminary version of the algorithm described. Determining the accuracy of the system was extremely difficult due to three innate flaws in the testing method. First, the data used for algorithm validation was hand-extrapolated from graphs, creating a high degree of inherent inaccuracy from the true resistance mean values for the chemicals involved. The data utilized was not only inexact, but was also extremely limited and did not exhibit the functional group resemblances necessary for effective comparisons. For example, in the extrapolation tests performed, the two chemicals correctly deduced had neighbors in the training set with the structural similarities required for extrapolation of identity. Toluene was surrounded by benzene, propanol, and freon, from which its molecular structure could be correctly deduced (Table 1, Table 3). Ethanol's neighbors were methanol, methane, and propanol, each of which share common structures with ethanol (Table 1, Table 3). For other chemicals such as ammonia, it was inherently impossible to extrapolate the correct identity since no other chemical in the training set shared a similar chemical formula. The low accuracy may have been in large part due to the limitations of the data set used for testing. With a large set of valid testing samples, the algorithm may prove to be more accurate.
Another cause of error may have been that the structural representation of chemicals utilized for analysis was overly simplistic. The program used Simplified Molecular Input Line Entry Specification, or SMILES, to perform string substructure searching. The SMILES notation's linearized ASCII string representations of chemicals appear to have been overly simplified for an in-depth analysis of chemical substructure. Using more complex molecular descriptors could greatly improve the accuracy of analysis, since functional groups and other similarities could then be extrapolated. External databases that provide set-defined search limitations and substructure searching could be utilized to provide more complex molecular modeling and searching. Although it was found to be impossible to precisely assess the accuracy of the program, with a large and authentic data set and a different molecular representation, the program's accuracy would be greatly increased. Using a larger set of physical characteristics as a basis of comparison and weighting may also prove more effective, as hypothesized by current research (Shevade et al. 2006). A neural network could be used to determine the outcome of such factors using the external database. With these factors, the accuracy of the algorithm could be improved to such an extent that it could be come a viable system for identification.
The algorithm proved to be reasonably efficient, processing a data set array of 100x32 in less than a hundredth of a second. Since the algorithm discards points after updating the clusters, it does not require more memory with an increased number of iterations through the operational stage. However, if greater efficiency were required, the implementation of more complex data structures could improve the processing speed. Firstly, in the cluster analysis, instead of utilizing an adjacency matrix to search for k-nearest neighbors, a kd tree could be used. kd trees map cluster data in a binary tree by point systems. Although they are complex structures, they would reduce the time complexity from O(n) to O(log n) (Yianilos 2000). In the substructure search, a "brute force" method was implemented in which each substring is searched within each of its neighbors. Instead, suffix trees could be used to limit the time complexity. These measures were not taken since the algorithm was found to be highly efficient without such added complexity. Even with the current implementation, the algorithm is efficient enough to act as a real-time analysis routine for robotic systems.
The potential practical applications of the algorithm are as diverse as they are useful. The main goal of the algorithm was to create a new, dynamic system of identification that could contend with previously unseen chemicals. This added feature can easily be integrated in present systems that use electronic nose identification algorithms and could improve reactions to unknowns while shortening the training stage. In military or safety situations, the practicality of a learning electronic nose algorithm is much more apparent. If a robot or sensor encountered an unknown odor in a real-world situation, it could not undergo the retraining stage required by standard pattern recognition algorithms. However, it could utilize the algorithm presented in this paper to analyze the unknown. Once the robot or sensor determined the chemical structure of the unknown, it could use the external database to analyze other potentially hazardous or important features, such as flammability or flash point. By hypothesizing the identity of the unknown, the robot or sensor could act more appropriately in the face of possible negative chemical properties. The novel use of an external database and dynamic cluster analysis creates a system that can adapt to scents and situations not previously encountered and practice dynamic learning. The algorithm proposed in this paper, through the use of hybridized cluster analysis and an external database, can dynamically adapt to, learn from, and react to previously unknown scents.
ACKNOWLEDGEMENTS
Many thanks to the National Science Foundation, the Pennsylvania Infrastructure Technology Alliance, and the Defense Advanced Research Project Agency for their sponsorship of the Lehigh Research Experience for Undergraduates: Learning through Nature. I am sincerely grateful to Dr. Margaret Ryan and her team at the Jet Propulsion Laboratory for providing research collaboration and for providing both sensors and data from JPL e-nose sensor tests. Many thanks also to Dr. N. Duke Perreira and Dr. Jennifer Swann for directing this REU experience.
REFERENCES
Brezmes, J. et al. (2003) Electronic Nose to Guarantee the Microbiological Quality of Bakery Product Manufacturing. Tenth International Symposium On Olfaction and Electronic Nose, 2003.
Brezmes, Jesús, et al. (2005) Evaluation of an Electronic Nose to Assess Fruit Ripeness. IEEE Sensors Journal 5: 1.
Burl, M.C., et al. (2002) Mining the Detector Responses of a Conducting Polymer Composite-Based Electronic Nose. First SIAM International Conference on Data Mining.
Busch, Michael and Benno Stein. (2005) Density-based Cluster Algorithms in Low-Dimensional and High-Dimensional Applications Fachberichte Informatik 45-56.
Carmel, L., N. Sever, D. Lancet, and D. Harel (2003) An eNose Algorithm for Identifying Chemicals and Determining their Concentration. Sensors and Actuators B 93: 77-83.
Chang, Hsaio-Te and Mu-Chun Su (2000) Fast Self-Organizing Feature Map Algorithm. IEEE Transactions on Neural Networks 11: 3.
Dutta, Ritaban, et al. (2002) Bacteria Classification using Cyranose 320 Electronic Nose. Biomedical Engineering Online 1:4.
Goodman, Rodney M. and Kea-Tiong Tang (2001) Electronic Olfaction System on a Chip. Proceedings on the 5th World Conference on Multi-Systemics, Cybernetics, and Informatics (SCI 2001) XV: 534.
Heaton, Jeff (2005) Understanding the Kohonen Neural Network. Introduction to Neural Networks with Java. Heaton Research, Inc.
Hines, Evor L, Pascal Boilot, Julian W. Gardner and Maria A. Gongora (2003) Pattern Analysis for Electronic Noses. Handbook of Machine Olfaction. Ed. T.C. Pearce, S.S. Schiffman, H.T. Nagle, and J.W. Gardner. Weinheim: 133-160.
Hopfield, J.J. (1999) Odor Space and Olfactory Processing: Collective Algorithms and Neural Implementation. Proceedings of the National Academy of Sciences.
Kumar, Vipin, Pang-Ning Tan, and Michael Steinbach (2006) Cluster Analysis: Basic Concepts and Algorithms. Introduction to Data Mining: 487-586.
Laha, Arijit and Nikhil R. Pal (2001) Some Novel Classifiers Designed Using Prototypes Extracted by a New Scheme Based on Self-Organizing Feature Map. IEEE Transactions of Systems, Man, and Cybernetics,Part B: CYBERNETICS 31: 6.
Lian, Nai-xiang and Yap-Peng Tan (2004) Probabalistic Approach to K-Nearest Neighbor Video Retrieval. Circuits and Systems, 2004. ISCAS '04. Proceedings of the 2004 International Symposium 2:193-6.
Llobet, E (2003) Dynamic Pattern Recognition Methods and System Identification. Handbook of Machine Olfaction. Ed. T.C. Pearce, S.S. Schiffman, H.T. Nagle, and J.W. Gardner. Weinheim:133-160.
Loutfi, Amy (2006) Odour Recognition Using Electronic Noses in Robotic and Intelligent Systems. Örebro University Library.
Moore, Andrew M (1991) An Introductory Tutorial on kd-Trees. Technical Report No. 209, Computer Laboratory, University of Cambridge.
Ryan, Margaret Amy, Hanying Zhou, Martin G. Buehler, Kenneth S. Manatt, Victoria S. Mowrey, Shannon P. Jackson, Adam K. Kisor, Abhihit V. Shevade, and Margie L. Homer (2004) Monitoring Space Shuttle Air Quality Using the Jet Propulsion Laboratory Electronic Nose. IEEE SENSORS JOURNAL 4: 3.
Shevade, Abhijit V. et al. (2006) Correlating Polymer-Carbon Composite Sensor Response with Molecular Descriptors. Journal of the Electrochemical Society 153: 11: H209-H216.
Siganos, Dimitrios and Christos Stergiou (1996) Neural Networks, the Human Brain, and Learning. Imperial College London: Surveys and Presentations in Information Systems Engineering.
Smith, Lindsay I (2002) A Tutorial on Principle Components Analysis. University of Otago, New Zealand.
Tryfos, Peter (1998) Cluster Analysis. Methods for Business Analysis and Forecasting: York University.
Vaid, Thomas P, Michael C. Burl, and Nathan S. Lewis (2001) Comparison of the Performance of Different Discriminant Algorithms in Analyte Discrimination Tasks Using an Array of Carbon Black,Polymer Composite Vapor Detectors. Analytical Chemistry 73: 321-331.
Yianilos, Peter N (2000) Locally Lifting the Curse of Dimensionality for Nearest Neighbor Search. Proc. 11th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA).
Zhou, Hanying, et al. (2006) Nonlinear Least-Squares Based Method for Identifying and Quantifying Single and Mixed Contaminants in Air with an Electronic Nose. Sensors 6: 1-18.