Author: Vijeth Iyengar
Institution: Tulane University, New Orleans, LA
Date: August 2006
Abstract
In this paper, we modeled the progressive loss of declarative memory in Alzheimer's disease (AD) using an artificial neural network (ANN) framework. Declarative memory is associated with tasks involving recognition. Furthermore, we modeled the declarative memory in a healthy individual as a fully connected Hopfield neural network. Memory loss in the healthy memory models was implemented by resetting randomly selected synaptic weights to 0'. Unhealthy memory models were created by damaging the healthy Hopfield memory models by a percentage of the weights. Recognition of the memory models was evaluated using recall/response rates. In the neural model, the detection of optimal network architectures was crucial. The paradigm that we have identified has three critical phases. The detection of neural synaptic promoters in the neural network was extremely imperative in the first phase of the investigation. In order to determine this, the network was trained on datasets and corresponding recall/response rates were observed. The second facet of the experiment involved the evaluation of different ANN's by which the optimal network architecture could be identified. And finally, the third facet, involved the detection of areas where synaptic connectivity was affected and where it could be improved. By comparing results of character/pattern recognition tests in normal and AD states, we showed that there is a possibility to strengthen connections in areas of the damaged network. Recall rates ranged from 88.75% for the healthy memory model and 49.98% for the unhealthy model.
Introduction
One of the most complex neuro-degenerative diseases is Alzheimer's disease (AD), a progressive form of presenile dementia generally affecting aged people. Alzheimer's disease is an irreversible, progressive disorder in which brain cells are damaged, resulting in the loss of cognitive functions such as judgment and reasoning, memory, and pattern recognition. Scientists estimate that by 2050 around 18 million people will be diagnosed with AD. Because of the growing scale, currently de facto incurability, and long agony of this chronic disease, finding a cure or better treatments for AD becomes increasingly important (Hughes 2003).
Figure 1: a) Model of a Hopfield learning algorithm under the influence of recurrent neural network architectures. Recurrent neural networks have been shown to be the closest to modeling associative memory in the brain than any other neural network architecture given that the neurons bi-directionally connect as human neurons do and not linearly. b) This schematic depicts a network with hidden layers (E4-E9; extra layers of neurons). This network increases the accuracy and processing power of a network.
Degenerated models of neural structure could be used to represent AD. In this paper, we propose a new model and correspondingly a new approach on this model to improve synaptic connections in neural structure. In the model neural paradigm, the detection of optimal network architectures was extremely important for the eventual cure of Alzheimer's. Our model has three phases. Phase one is detection of neural synaptic promoters. For this, we trained the AutoAssociative Neural Networks (mainly Hopfield Neural Network) on different training datasets and observe its recall and response by measuring its prediction accuracy on test datasets. This type of network is found in Figure 1.
Phase two is evaluation of performance of different artificial neural network, by which the optimal network architecture for neural synaptic activity could be found. Phase three used results from Phase two to find areas where synaptic connectivity is present and where it can be improved. By comparing results of character/pattern recognition tests in normal and AD states, we showed that there is a possibility to strengthen synaptic connection in areas of the damaged network and an opportunity to cure AD or at least alleviate AD symptoms.
We modeled the progressive loss of declarative memory in AD using an artificial neural network (ANN) framework. Declarative memory is associated with tasks involving remembrance and recognition of facts from past experience and learning. We model the declarative memory in a healthy person as an associative memory implemented using fully connected Hopfield neural networks (healthy memory models) (Knight 2002). Two versions of Hopfield networks: (1) Hopfield-1 and (2) Hopfield-2 were used in our experiments. The healthy memory models consist of thirty-six nodes with a maximum recall capacity of 4.968 (approximately five patterns). Learning process in a healthy biological memory is simulated by training the memory models using Hebb's rule on five input stimuli (patterns) from experimental character recognition data prepared in our laboratory (Werness 1993). Training in the memory models involves asynchronous iterations of input patterns until the response of all nodes in the network stabilize. Progressive loss of remembrance and recognition in the healthy memory model is achieved by gradual degradation of the randomly selected synaptic neural connections. (Dalla Barba 1997, Squire 1992). Recognition and remembrance of the memory models are evaluated using recall and response measures. The recall rate of a memory model is defined as the percentage of input patterns recalled correctly when tested on input patterns. The response rate of a memory model is defined as the percentage of patterns correctly identified when tested on separate test data.
Our study has developed: (1) a network that mimics normal patient neural connectivity, (2) a more profound understanding of how the connectivity relates to functional processes such as pattern recognition and memory, (3) a model that computationally represents AD states, and (4) initial identification and modeling of areas of connectivity susceptible to Alzheimer's problems and determination of how functional improvements could overcome these deficiencies. We still need some biochemical techniques to transform our achievements back to AD treatment. However, a good model creates correct understanding; the latter will lead to a right theory. Future work could include testing the model with clinical data, especially data on facial recognition, which is a common problem in AD.
In the first year study, we utilized feed-forward neural networks as a basis of constructing a healthy biological neural network. Feedforward neural networks are composed of layers of neurons in which the input layer of neurons are connected to the output layer of neurons. Two types of learning in feedforward networks are Back-Propagation and Perceptron learning. Back-Propagation learning filters errors in the network's prediction accuracy until accuracy is efficient. A Perceptron learning environment results in a simple output from an input neuron (Albus 1971). From the first year study, we were able to produce 1) A healthy network and 2) A network with minimally damaged network connections. Upon further review, feed forward networks were discovered as crudely simulating human memory processing. In the second year study, we utilized recurrent neural networks. Recurrent neural networks are a model with bi-directional data flow, allowing direct communication and transfer of information between two neurons. Recurrent neural networks have known to be an extremely efficient model of human memory. A Hopfield network is a recurrent neural network in which all connections are symmetric (Amit 1989). Because of the capabilities of the Hopfield Network in closely simulating human associative memory, we performed experiments using the Hopfield neural network (Amari 1989, Anderson 1972, Knight 2002).
Alzheimer's disease (AD) is an irreversible, progressive disorder in which brain cells (neurons) are damaged. The human mind has been known to occupy more than 1 billion neurons at a time. The reasoning capabilities of a person are extremely dependent upon these neurons because of their signaling and "information transfer" abilities. If there exists neuron connectivity "deficiencies," most scientists agree that thinking and reasoning capabilities would go astray and prevent individuals from performing common duties. As neural connectivity declines, memory also suffers. As AD affects the brain, nerve cells stop functioning properly, which then causes short term memory to fail. As short term memory fails; a person's ability to perform common tasks starts to deteriorate (Graham 2003).
An artificial neural network (ANN) is a system inspired by the human brain. Its design is based on a multiple layer network consisting of neurons. These neurons are then connected to neighboring neurons with varying strengths of connectivity power. Neural networks are closely related to the structure of the brain, and it is utilized in neuroscience and computational neuroscience. The computational neuron, which composes the bulk of artificial neural networks, receives certain inputs and then produces certain outputs. It is the basic unit of artificial neural networks. Artificial neural networks conform to the following design: a string of axons "carrying" certain information weight inputs is connected to a parent neuron; then the parent neuron sums up the information weights of each input; finally the output represents the total sum of information weights from the inputs. Artificial neural networks are usually designed as a multilayer network in which layers connect to each other. There is first an input layer that receives an exogenous input from an external source in environment (usually a user) and then an output layer, which gives the desired result. Artificial neural networks often take on the form of a two-tier network; however, to improve the strength of the network architecture, a third layer is employed between the input and output layers. This layer is called the hidden layer and is used to enhance a network's performance. A hidden layer is important because it provides increased connectivity between the neurons. Under a limit, the more hidden layers a network has, the more powerful the network will be (Anderson 1983).
Communications are vital for relaying information from one neuron to another. In an artificial neural network, neurons are connected via a network of paths carrying the output of one neuron as input to another neuron. These paths are normally unidirectional; there might, however, be a two-way connection between neurons if one input goes in the reverse direction. A neuron receives input from many neurons, but produces a single output, which is communicated to other neurons. Connections provide in humans the ability to reason, but in an artificial neural network an ability to reach the desired result. (Anderson 1983, Amit 1989).
When a network does not perform correctly, we adjust information weights assigned to connections, and consequently the network "learns" from the adjustments since it enhanced its performance. Learning in a particular neural network is dependent upon the architecture type of the neural network (Albus 1971).
Unsupervised learning involves hidden neurons that have to organize and process data without help from the outside. In this approach, no sample outputs are provided to the network against which it can measure its predictive performance for a given vector of inputs. This is "learning by doing." Reinforcement learning includes connections among the neurons in the hidden layer that are randomly arranged, then reshuffled as the network is told how close it is to solving the problem. (Werness 1993, Amit 1989).
Methodology
Models and Approaches
We used a number of important neural network concepts to fashion our version to model normal and diseased brain connectivity. In the first year study, we used backpropagation learning because the network filters the errors that occur within the network and adjusts its connections to learn better. Often learning technique use various forms of learning rule. A learning rule is a mathematical algorithm that updates connection weights and controls learning by a network. Learning rules are important because they usually describe the relationship between a neuron and the inputs involved.
The following learning rules are commonly used in artificial neural networks: Hebb's Rule specifies that if a neuron receives an input from another neuron, and if both are highly active, i.e. mathematically have the same sign, the weight between the neurons should be strengthened. Delta Rule changes connection weights in the way that minimizes the mean squared error of the network. Basic idea of this rule is to continuously modify strengths of input connections to reduce the difference (delta) between the desired output value and the actual output of a neuron. The error is back propagated into previous layers, one layer at a time. The process of back-propagating network errors continues until the first layer is reached. Therefore the network is called feed forward / back-propagation. In this paper we plan to use backpropagation learning coupled with Hebb and Delta learning rules, which provides a tool in determining optimal network structures. In this paper M₁ - E₁, represented the learning (M₁) and the learning rule (E₁) for our network architectures. In the second year study of this project we utilized the Hebb Learning Rule for our Hopfield Network.
The following diagrams are mathematical models of learning algorithms used in this experiment: SingleLayer Perceptron (a,b), Multi-Perceptron (c) and BackPropagation architecture (d) are presented in Figure 1.
Figure 2: a) This depicts the first artificial neuron model developed by McCulloch-Pitts. This model has no information weights (synapses) and a threshold function (u) needed to be satisfied for the neuron to fire. There are 5 outputs (x1.xn+m) and an output represented by d1. b) Perceptron network is typical network architecture of a single layer. This is the most primitive of network architectures. In this figure, three inputs (x1.xn) are given into the network with designated information weights (w1.w3) acting as synapses. The circular representation depicts the node (nerve cell) of the network. The subsequent output is designated as y. c) This figure depicts higher order two-tier perceptron network architecture. There is present the same number of inputs, but an increase in the number of nodes (neurons) and thus, more connections. This network will yield three outputs. Compared to Figure1a, there are more number of connections thus increasing the processing power and accuracy. d) Here we show a three-tier network with four inputs and two outputs resembling a typical Back-Propagation (BP) network architecture. There are more layers of neurons compared to previous figures because of the increase in inputs. BP is unique in that errors that are produced in the network are filtered back into the processing unit to improve the accuracy of the network, leading to the "unsupervised" learning environment.
A More Refined Model for Human Memory
Autoassociative neural networks are a type of artificial neural networks detailed in human memory. Autoassociative networks can store single instance items and very accurately represent human memory. This aspect of artificial neural networks is extremely important because it plays a vital role in pattern recognition. One characteristic of networks at pattern recognition is iterations (repetitions). The greater the number of iterations, the better a network is at recognizing patterns. The basic design of an autoassociative neural network consists of a two-tier layer network, each layer representing an external environmental source. This makes it easier for a user to input data and receive an output. This is supported by previous findings (Shun Ichi 1989).
In the twotier system, there is a layer of "world" units and a "layer" of learning rates. The world units represent the input data from an external environmental source and the learning layer represents processing of the network to produce an output. To test a network for pattern recognition we first create a healthy biological neuron; then we will create a parity generator and a character recognition test. These tests will allow us to measure the network's prediction accuracy. Datasets of 5 binary numbers (zeros and ones) are added to the network. In the parity generator, the user, before giving the numbers to the network, randomly predicts the result to test the network's ability in predicting the user's result, which is based highly on pattern recognition. In the character recognition test, we tested the network on a group of characters, mainly alphabets. These characters were comprised of bi-polar numbers (-1, +1) and the network was responsible in recognizing the character by finding patterns within the bi-polar numbers that made up the character.
Obtaining an Optimal Network Architecture
This subsection describes means to detect neural synaptic promoters by identifying optimal network architecture. We performed tests on character recognition and pattern recognition. We first constructed a healthy biological network. We then determined whether a network was healthy or not by using a parity generator and the observation of prediction accuracy. If the prediction accuracy was over ninety percent, we defined it as a healthy system. Anything below ninety percent was an unhealthy system. After determining healthy network systems, we performed pattern and character recognition tests on the other varying networks (Mi Ei) to find the optimal network structure among (Mi Ei).
The Mi Ei was used to measure the performance of a network. The Mi Ei represented varying models of learning rules and network architecture. In combining the various learning rules, we hoped to determine the best type of network architecture. In assessing the accuracy of these models, we hypothesized that the optimal architecture would possess highly probabilistic regions of neural synaptic promoters.
We tried to determine whether we could improve unhealthy biological systems by using the optimal network architecture. We gradually degraded the weights until prediction accuracy and accuracy in other testing areas (pattern and character) went from 90 percent to 40 percent. Determination of the optimal architecture depend on if the architecture could improve the accuracy of an unhealthy biological system to that of a healthy biological system. We measured the performance of our neuron model Mi by its prediction accuracy or by a normalized sum of squared errors over the test data. Other parameters for measuring the performance are the number of iterations versus the prediction error.
ANN Mimicking a Healthy Biological Neural System
We modeled a healthy biological neural network as a two-tier fully connected network with Ei as basic learning units. An Ei is a 5-layer ANN with one input layer, one output layer, and three hidden layers. Ei is a multi-layer neural network that uses the delta rule for learning. Similarly Mi is also modeled as a 5-layer neural network with one input layer, 3 hidden layers, and a single output layer.
Simulation Results
article_756_order_3
We will first discuss the results attained from last years study. We trained two neural networks (1) Perceptron network, and (2) Back-propagation network on the data generated by a 4-bit parity generator. Table 1 below gives the data generated by a 4-bit parity generator. The prediction accuracy of Back-propagation neural network is 100%. The prediction accuracy of Perceptron neural network is 80%. We made graphs that depicted the number of iterations needed for each learning algorithm. The more number of iterations needed the better prediction accuracy the model produced.
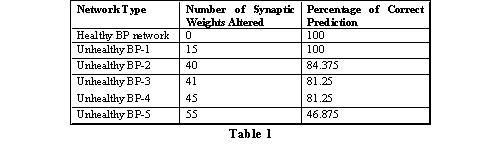
This report presents the results of damaging a healthy back-propagation type neural network model by altering its post-convergence synaptic strengths (weights). The healthy back-propagation type neural model is damaged to mimic the weakened synaptic neural connections in the brain of an Alzheimer's patient. The fully connected architecture of our healthy back-propagation type neural network consists of five neurons in the input layer, twelve neurons in the hidden layer, and one neuron in the output layer (resulting in 66 synaptic weights). The healthy network was trained on 5-bit parity generator dataset to produce 100% accurate prediction. The healthy network was iterated 10,001 times to reach its convergence. We present the results of one healthy back-propagation type neural network and five unhealthy neural networks (in terms of its prediction accuracy) obtained by damaging the healthy neural network. To obtain an unhealthy network, some weights of the healthy model were altered to random values and the new network thus obtained was trained for 10,001 iterations. From Table 1, we may observe that as the number of altered synaptic weights increase, the prediction accuracy decreases.
Our neural network has been trained with three different sets of initial weights w1, w2, w3, with two different learning rates 0.1 and 0.5. Results in Table 2 show that the back-propagation network performs well if trained on 100% of the dataset. However, the prediction accuracy degrades as the percentage of training data is reduced to half the original dataset. It can also be observed that as the learning rate decreases, the number of iterations (epochs) increases.
Second Year Study Results (With Hopfield Network)
Following diagrams show comparison of recall and response rates of two healthy networks and seven unhealthy networks with increasingly monotone damage. Results are reasonable and for the most part fall in our prediction based on the above theory. For healthy network model Hopfield-1, in both recall and response rates, only 10% damaged network model is intractable, most damaged models have worse performance, and the divergence increase as damage level increases. For Hopfield-2 recall data, there is not much difference between the healthy model and unhealthy models. However, in response rate, data is very similar to Hopfield-1. Generally, we can safely say simulation data met our theory and analysis logic well. The results can be seen in a chart of graphs, listed in Figure 2.
Figure 3: A set of figures, numbered that show the progressive network performance vs. the number of connections that we continuously damaged. The damage was done through random synaptic pruning and was done at an increasing rate in order to determine the network's sustainability and robustness. The last two figures, figures e and f show the overall comparison of the Hopfield one with Hopfield-1 healthy network versus Hopfield 2 healthy network, and one with Hopfield-1 healthy network versus the various percentages of damaged networks
Recall and response rates of Hopfield-1 and Hopfield-2 memory models were computed on character recognition data containing five training patterns and fifteen test patterns representing characters a', b', c', d', and e'. Each input pattern is a six-by-six matrix vector containing bipolar values (1' indicates an active node and -1' indicates an inactive node). Memory loss in the healthy memory models is implemented by resetting randomly selected synaptic weights to 0'. A Gaussian random number generator was used to select the weights to be degraded. Fourteen unhealthy memory models were created by degrading the healthy Hopfield memory models by 10%, 15%, 20%, 25%, 30%, 40% and 50% of the weights. Each unhealthy memory model represents stage-by-stage progressive degeneration of synaptic neural connections in AD. The recall and response of all healthy and unhealthy memory models over a varying number of input patterns was observed. Average recall rates obtained by varying the number of input patterns for Hopfield-1 ranged from 88.75% for the healthy memory model to 49.98% for the 50%-unhealthy model and the average response rates varied from 63.19 for the healthy model to 18.91 for the 50%-unhealthy model. Similarly, the average recall rates for Hopfield-2 network ranged from 57.08% for the healthy memory model to 44.58% for the 50%-unhealthy model and the average response rates varied from 46.67% for the healthy model to 40.41% for the 40%-unhealthy model.
All simulations were programmed in MATLAB. The basic point is to make a comparison between a healthy Hopfield network and an unhealthy diseased network, whose recognition accuracy was below 90%. Our experimental results indicated that by introducing different learning algorithms into the existing diseased network architecture, recognition accuracy of 50-80% can be improved compared to the original architecture. Detailed simulation results are reported.
Discussions and Conclusions
This paper introduced a novel technique in assessing a way to improve neural synaptic promoters in disease with AD. This was achieved by utilizing an artificial neural network which emulates information processing within the brain. By detecting the best learning (neuron design) mechanism we were able to detect areas where connectivity will be strengthened. We also damaged certain neuron designs by altering information weights that emulated information processing within AD. This is important because previous studies and research tried to improve neural synaptic connectivity in healthy networks, while this paper tried to improve neural synaptic connectivity in unhealthy (Alzheimer's) networks. We were able to come up with the following conclusions that are very vital in the future study of curing AD:
First Year Study Results:
In prediction accuracy, the Back Propagation Learning Architecture gave a 100 percent prediction accuracy (healthy network) and Perceptron yielded a 80% prediction accuracy
We observed that if we decreased the number of data given to the computer the prediction accuracy goes down
As the learning rate decreases the network takes more time to process information
In our process of degradation of BP network, 40 - 45 weights needed to be spoiled in lowering the prediction accuracy This means that BP is the most efficient learning network.
Second Year Study Results
Average recall rates obtained by varying the number of input patterns for Hopfield-1 ranged from 88.75% for the healthy memory model to 49.98%
Similarly, the average recall rates for Hopfield-2 network ranged from 57.08% for the healthy memory model to 44.58%
The unhealthy network character recognition performance was improved from 44.58% to over 50%. This proved that utilizing varying learning algorithms such as Back-Propagation and Hebb Learning would improve recognition in networks that have been damaged. In Figure 2, in graph c, there is represented a result where a 15% damaged network had the same level performance as an unhealthy network.
In the first year study, the back-propagation learning mechanism was the most robust network found in the first year study. This statement is validated by the fact that our experimental results told was that over 40 weights was needed to be changed in order to decrease the prediction accuracy. In the future we plan to use clinical data of AD and input this data into our established networks. The results of this investigation will be to validate our networks with clinical data from AD.
Clinical Applications
1.Better imaging techniques for doctors in assessing brain abnormalities brought about by AD.
2.An accurate model of the effects of gradual neuron deterioration in patients with Alzheimer's, eventually leading to better statistical/mapping databases in hospitals.
3.Models enabling doctors/scientists to explore areas of the brain where possible improvement of neural synapses damaged could occur.
Therapeutic Applications from this Study in patients with AD
1.Minimizing new memory load (To minimize the amount of memory in AD, a large memory may lead to synaptic deletion)
2.Strengthen old and existing memories (By laying a firm foundation on existing connections, existing memory synapses may get better)
3.Using Biofeedback techniques for the control of physiological processes in AD patients
Acknowledgements
I sincerely acknowledge the assistance and guidance of Dr. Vir Phoha and his graduate student, Kiran Balagani at Louisiana Tech University. Without the support providing by Dr. Phoha and Kiran I truly believe this research endeavor would not be achieved. The constant encouragement and scientific discipline I cultivated in their labs was extremely vital in my future career as a scientist and doctor.
Citations/References
[1] Albus, J. S. (1971). "A Theory of Cerebellar Functions," Mathematical Biosciences, 10, 25-61.
[2] Alkon, D. L., Blackwell, K. T., Vogl, T. P., and Werness, S. A. (1993). "Biological Plausibility of Artificial Neural Networks: Learning by Non-Hebbian Synapses," in Associative Neural Memories: Theory and Implementation, M. H. Hassoun, Editor, 31-49. Oxford University Press, New York.
[3] Amari, S.-I. (1989). "Characteristics of Sparsely Encoded Associative Memory," Neural Networks, 2(6), 451-457.
[4] Amit, D. J. (1989). Modeling Brain Function: The World of Attractor Neural Networks. Cambridge University Press, Cambridge.
[5] Anderson, J. A. (1972). "A Simple Neural Network Generating Interactive Memory," Mathematical Biosciences, 14, 197-220.
[6] Anderson, J. A. (1983). "Neural Models for Cognitive Computations," IEEE Transactions on Systems, Man, and Cybernetics, SMC-13, 799-815.
[7] Dalla Barba G, "Recognition memory and recollective experience in Alzheimer's disease", Memory. 1997 Nov; 5(6):657-72.
[8] Haist F, Shimamura AP, Squire LR, "On the relationship between recall and recognition memory", J Exp Psychol Learn Mem Cogn. 1992 Jul; 18(4):691-702.
[9] Humphreys MS, Dennis S, Maguire AM, Reynolds K, Bolland SW, Hughes JD; "What you get out of memory depends on the question you ask", J Exp Psychol Learn Mem Cogn. 2003 Sep; 29(5):797-812.
[10] Lee AC, Rahman S, Hodges JR, Sahakian BJ, Graham KS "Associative and recognition memory for novel objects in dementia: implications for diagnosis", Eur J Neurosci. 2003 Sep; 18(6):1660-70.
[11] Shun Ichi Amari. Characteristics of Encoded Associative Memory. Springer Verlag 1989, 1989.
[12] Smith JA, Knight RG, "Memory processing in Alzheimer's disease", Neuropsychologia. 2002; 40(6):666-82.